Content-Type: text/shitpost

OR SUFFER THE UNSPEAKABLE CONSEQUENCES

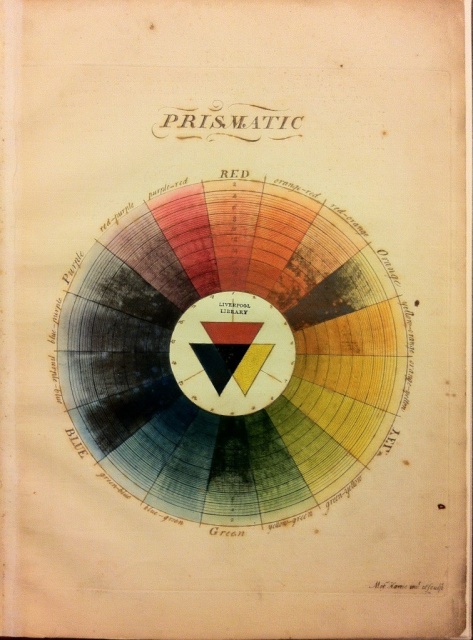
Incidentally, Harris’ The Natural System of Colours has more than one plate. In addition to the one depicting the “prismatic” colors, starting from the primaries red, yellow, and blue, and showing how they mix to form the secondaries orange, green, and purple, he has a second plate that starts with the secondaries and mixes them to form tertiaries.

Harris names the tertiaries “olave” (orange-green), “slate” (green-purple), and “bronn” (purple-orange). I think “olave” and “bronn” are just alternate spellings of “olive” and “brown” but it is after midnight and I do not want to go downstairs to get out the Big Dictionary.

Wikipedia asserts that the terms “citron”, “slate”, and “russet” have since become common, and attributes them to George Field's Chromatography (1835). Field actually calls them “citrine”, “olive”, and “russet”.

Here is a page from Moses Harris’ extremely influential book The Natural System of Colours, published around 1760. This image is widely reproduced and you may have seen it before:

(This particular image is from a copy of the second edition of 1811, and as you can see it has suffered significant damage.)

I have wondered about this for decades now: Why is the label for yellow written backwards?

More progress on counting paths on octahedra! Suppose you want to know how many paths of length !!n!! there are between two opposite vertices of an octahedron.

It turns out that it is the same as the number of ways to take !!n!! terms, each of which is either !!\pm1!! or !!\pm2!!, and add them up to get an odd multiple of 3. (Order matters.)

For example, there are 8 paths of length 3, which correspond to !!1+1+1, -1+2+2, 2-1+2, 2+2-1,!! and their negatives.

That actually seems like an improvement because it seems like counting those sequences will be a straightforward application of generating functions.