Mark Dominus (陶敏修)
mjd@plover.com
I have another blog that doesn't suck.
Archive:
| 2023 | JF |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFM |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | ND |
Comments disabled
The miner should not start mining operations in a district which is oppressed by a tyrant.
— De re metallica, 1556
The New York Python conference PyGotham is trying an experiment: they're letting the community vote on the (suitably anonymized) talk proposals. Interesting idea!
But I think they're asking the wrong question:
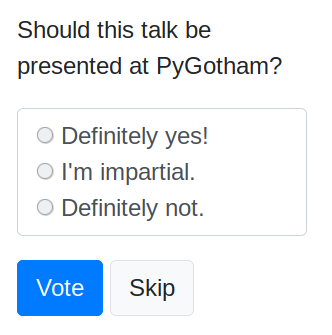
I think it should say instead:
If this talk were presented at PyGotham, would you attend?
⭘ Yes
⭘ Maybe
⭘ No
If I were running a conference, I would care deeply about what people wanted to see, and very little about what they imagined that other people might want to see.
Standard !!\TeX!! has a control sequence, \ominus, which produces the symbol
!!\ominus!!. (It is analogous to \oplus !!\oplus!!.)
For a while, at a time when I was writing more !!\TeX!! than I do now, I would sign my documents as !!\text{Mark D$\ominus$}!!.
Alicja Raszkowsa nerdsniped me into inquiring into pangrams in languages other than English. The Polish Wikipedia page has an extensive list. I was interested to learn that in Polish, a pangram must contain each of ‘z’, ‘ż’, and ‘ź’. Note that this is not completely obvious. A Spanish pangram must contain both ‘n’ and ‘ñ’, but need not contain both ‘o’ and ‘ó’, as those are the same letter. Possibly fun exercise: write a computer program which, given a sequence of pangrams in an unknown script, emits the list of letters in that script. For Spanish it should emit both ‘n’ and ‘ñ’, but only one of ‘o’ and ‘ó’.
So far my favorite find has been this Reddit discussion of the perfect Finnish pangram
Törkylempijävongahdus
which contains each Finnish letter exactly once. It appears to mean the act of a filth-lover pleading with someone to sleep with them.
The best part of the discussion was when one Finnish user complained that they did not know what “vongahdus” was supposed to mean. Another user explained:
Vongahdus as in something a vonkaaja would do.
This was accepted without any request for further clarification. Instead the first user's reply was:
I just love our language, everything is as confusing as possible.
Just as the phrase “what the entire fuck” implies the existence of fractional fucks…
The professor said to me that analysis was a deep enough and rich enough subject that I would not be wasting my time to take it again, and that I would not be bored. I thought about this a little bit, and I thought about this a little bit, and then I agreed that he was probably right.
I have something to add to this. All through high school I fought with my high school math department to be excused from high school math. For example, I said it was stupid to be taking high school trigonometry while also studying differential equations at Columbia. My tenth-grade trigonometry teacher said that just because I was studying differential equations at Columbia, did not mean I did not also have something to learn from tenth-grade trigonometry.
Looking back on it now, with the wisdom that comes with age, I can see that I was right and he was wrong. I had nothing to learn from tenth-grade trigonometry.
My ninth-grade math teacher asked why I was always “trying to do an end-run around life”. I suppose that to this ninth-grade math teacher, your ninth-grade math class is one of life's highlights, one of those fleeting moments of youth that one must stop to savor lest it slip away all too quickly.
But I think this story proves that I wasn't just trying to rush ahead for the sake of rushing ahead. When I was offered the chance to do two semesters of real analysis a second time, instead of rushing ahead to the next thing, I didn't try to skip it. I didn't even argue.
Those high school people were wrong. So, so wrong.
May they all burn in hell.
[ This is another resurrection of a deleted Math Stack Exchange post. There's nothing really wrong with it, except that I feel like it's not of general interest. ]
Which parts of real-analysis are worth studying if you have already taken several calculus courses? I know that real-analysis is more 'rigurous', but still I wonder whether it is worth to again go over a lot of subjects that I already know from through calculus.
When I first entered university, shortly before classes began, I met with an professor whose task was to advise me on which classes to take in my first semester. After hearing me describe my background, which included passing the college-credit calculus exam at age fifteen, he suggested that I take real analysis.
“But I took that already,” I protested. “I had a two-semester course in real analysis at Columbia University last year. We used the little blue Rudin book. I got A’s.”
The professor said to me that analysis was a deep enough and rich enough subject that I would not be wasting my time to take it again, and that I would not be bored. I thought about this a little bit, and then I agreed that he was probably right. So I took the analysis course again. We used the same textbook, but I was not bored, and it was not a waste of time. It was an extremely good use of time; I have never regretted it.
So that's my answer about which topics of real analysis should be studied if you have already done calculus: all of them. You will not be bored, and it will not be a waste of time, because the answer is the same even if you have already taken real analysis.
[ The following is ill-informed speculation. ]
I think that in some dialects of American English, “well” is sometimes pronounced with a final glottal stop, /wɛlʔ/. People wanted to represent this pronunciation in writing, but they couldn't, because English doesn't have a way to write a glottal stop, so instead they started to write it instead as “welp”. Once that spelling had been written and read enough times, people actually started to pronounce it /wɛlp̚/ or /wɛlp/.
Bonus question: if any of this is correct, why is it spelled “welp” and not “welk”?
