Content-Type: text/shitpost

Subject: The fickle gods of math Stackexchange
Path: you!your-host!wintermute!uunet!asr33!hardees!triffid!mechanical-turk!berserker!plovergw!plovervax!shitpost!mjd
Date: 2018-02-04T12:34:18
Newsgroup: talk.mjd.math.se-gods-fickleness
Message-ID: <3afeea89031c86b6@shitpost.plover.com>
Content-Type: text/shitpost

I got a bunch of upvotes this week for garbage posts, but none for my favorite post. OP presented an ugly cubic graph with ten vertices:

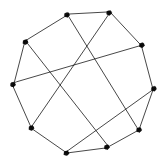
$The ugly graph has vertices 0, 1, …, 9 arranged in a ring, with five additional edges: 1–5, 2–8, 3–9 4–7, 5–10$

OP asked if this ugly graph was isomorphic to the Petersen graph:

$The petersen graph has two sets of five vertices each. Each set is connected into a pentagonal ring. There are five more edges between vertices in opposite rings, but instead of being connected 0–0 1–1 2–2 3–3 4–4, they are connected 0–0 1–2 2–4 3–1 4–3.$

Often the answer to this sort of question is “poke around until you find some ad hoc property that one graph has but not the other. Usually you start by counting up the vertex degrees, which must match. In this case, both graphs are cubic, so that doesn't help. Someone else tried the next thing and found that the ugly graph has a 4-cycle, which the Petersen graph does not, question answered.

But my answer was more elegant. The Petersen graph has many interesting properties. Among other things, it is the smallest non-hamiltonian cubic graph. But the ugly graph obviously has a hamiltonian cycle —the ring around the outside — so it's not the Petersen graph.