Mark Dominus (陶敏修)
mjd@plover.com
I have another blog that doesn't suck.
Archive:
| 2023 | JF |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFM |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | ND |
Comments disabled
Via Pervocracy: “I found it: the best scientific diagram”.
Can we infer from Wesley's name that he and Dr. Crusher are Methodists?
(Asking such questions is perilous, because someone might show up at my door with a 58-page summary of past and current scholarly thought on the subject.)
From Chris Siebenmann's blog:
The reality of sysadmin life is that in many situations, there are too many obvious problem causes to keep track of them all.
I recommend this blog.
Orin Kerr of the Volokh Conspiracy blog has written an article on how to read a legal opinion. I have found reading federal court opinions fascinating and educational. U.S. federal judges are almost always intelligent and thoughtful, and excellent writers. I recently wrote:
Even when I disagree with the decision, I almost always concede that the judges have a point. It often happens that I read the decision and say “of course that is how it must be decided, nobody could disagree with that”, and then I read the dissenting opinion and I say exactly the same thing. Then I rub my forehead and feel relieved that I'm not a federal circuit court judge.
As dense technical material, law opinions are unusual because their underlying topics are public policy issues that affect everyone, or everyday issues as property disputes and interactions with the police. So they have a relevance that, say, scientific or engineering material does not. If you really want to know what the Supreme Court said recently in connection with Masterpiece Cakeshop, you are not going to do better than to read what they actually said about it.
But like other dense technical material, court opinions are full of obscure jargon. Kerr's article explains the most important parts of this jargon and describes the overall structure of the opinions. If you think you might be interested in reading some Supreme Court opinions, but you find it hard to get your feet under you, you might give Kerr's article a try.
The Philadelphia Inquirer reports today:
The Pennsylvania Supreme Court on Friday ordered the release of a redacted copy of a highly anticipated grand jury report on clergy sexual abuse, one the court said identifies more than [some number of] “predator priests”
The number boggled me.
It was given as “more than 300”. Holy cow. And this is only for six of Pennsylvania's eight dioceses. Philadelphia and Altoona-Johnstown were investigated previously.
Had I been greatly underestimating the number of priests in Pennsylvania, I wondered. No, there are 792 in the Philadelphia Archdiocese and 207 in the Pittsburgh Diocese. The six dioceses in the report couldn't have more than 1200 priests total.
I am speechless with rage and disgust.
[ Addendum 20180817: I tried to estimate what fraction of all priests were mentioned in the report and guessed around 6%. ]
Another writer I was able to track down was Isabelle C. Chang, author of the Chinese Fairy Tales I had enjoyed as a child.
I learned that Chang had been an indirect but important contributor to the development of the combined oral contraceptive pill. The National Academy of Science biographical memoir of her husband, Dr. Min Chueh Chang, says:
Much credit must be given to Chang’s talented wife for her willing acquiescence in the role of a Confucian wife as her part in enabling Chang to develop his full potential unhindered by domestic concerns.
Ms. Chang worked as a writer and librarian, raised their three kids and took care of their house, while Dr. Chang worked relentlessly and successfully on the problem of using steroids for birth control.
One of the authors I rescued from the ruins of my childhood memories was C.A. Stephens. I had read one story of his, called “The Jonah”, and found it delightful. An earlier draft of this article recounted the story, but it is better for you to read it yourself. The background is that five cousins, are living with their grandparents on a farm in Maine, and the grandparents are out of town for the week.
Thanks to the Internet, I was able to find out who wrote this, and get his books out of the library. Not all the stories were as delightful as that one but many of them were, and now I am a C.A. Stephens fan.
Check it out.
An important thing to keep in mind is that the old-style imperial fuckload is actually 14% larger than the metric fuckload.
AO3 has only one story about Mondamay the Potter, and it is in Russian.
Also, where the hell is my Sonar Taxlaw fanfic?
By the way, Martin Wells says, in Octopus: Physiology and Behaviour of an Advanced Invertebrate (Springer, 1978) that contrary to popular report, octopuses cannot learn to open jars:
Crabs can be wrested from containers (Pieron, 1911; Schiller, 1948; Cousteau and Diole, 1973) but the results appear to be achieved by chance and there is little indication that the octopus can learn to deal with the situation more efficiently with practice. The animal approaches and struggles with the apparatus until something happens; if it learns any-thing as a result of its experience it is only to be more persistent and vigorous.
(p. 241)
There may have been further developments since 1978, of course.
Yesterday I went to breakfast at a restaurant and unexpectedly ran into Lorrie who was just finishing her own breakfast. I brought Placido the octopus out of my bag to say hi, and she took a picture of him sitting on my shoulder.
The waitress happened by and asked “what is that for?”
I said “Catching crabs. Opening jars. Hiding in small spaces.”
I don't know what she was asking, but that seemed to satisfy her.
I want to use this story in a future article about novices with inaccurate mental models.
When I was a young teenager, I had a Commodore 64 computer. It could do bitmapped graphics. You would tell it which pages of memory should be displayed on the screen, and then poke bytes into that region of memory to switch the dots on and off. I had a lot of fun with this.
I did not have a dedicated monitor. Instead I had an old color TV that the computer used as a display. There was a device on the back of the TV that switched it between displaying the computer output and displaying the received TV signal. One day I had a wonderful idea: I would switch the device to TV mode and put on some TV program — I imagined Star Trek specifically. Then instead of poking data into the computer memory to make dots appear on the screen, I would read the memory into a file to get a screenshot of the TV program.
I didn't expect that this would work well; I thought if it worked at all there would be a huge amount of sampling skew, because the TV image would change drastically during the memory copying process. But I hoped the results might be interesting anyway, and at least part of it might be partly recognizable.
Of course, it didn't work at all. The connection from the computer to the TV was entirely one way. The device on the back of the TV was an RF modulator, which transformed the computer's video output into a fictitious radio signal that the TV would interpret. Switched into the TV position, the computer's video output went nowhere. In no case was the TV image accessible to the computer. My program to read the contents of the bitmapped memory read nothing but zeroes.
I think it's useful to remember times like this when I was so utterly confused about what was really happening.
I was once talking to a recruiter about some programming job. He asked me to rate my programming skills on a scale of 1 to 10.
I was perplexed. “How is that distributed? Should there be an equal number of people in each group? Or does someone get a 10 if they're five standard deviations above the mean? Or what?”
Now he was perplexed. “Uhhh, nobody's ever asked me that before. Just interpret it how you like.”
“In that case I'm a 10.”
Another cool piece of Dionysian paraphernalia is the thyrsus (from Greek θύρσος) which is a staff topped with a roughly conical plant part, canonically (cononically?) a large pine cone, but it could be a flower or an artichoke or something like that.
I have sometimes toyed with the idea of carrying one around, but it seems like it would be more inconvenient than useful.
In Doorways in the Sand the donkey is named “Sibla”, which I was thinking would be a good name for the donkey of Silenus. But then I remembered that actually Sibla is not really a donkey, but an impostor. (“The real donkey is tied up out back,” he says.) Probably Silenus had a series of donkeys, each named differently. What did they do with the donkeys when they died? (Peacfully, I imagine, at advanced ages.) I hope they buried them honorably.
One of my favorite lines from the book is in connection with Sibla:
"Go to hell," I said. "My uses for telepathic donkeys are limited.”
Haven't we all felt that way at one time or another?
I find that somehow, in twelve years of blogging, I have never mentioned Doorways in the Sand. I will have to discuss it at some point.
Today a co-worker mentioned the word “euouae”, which are a certain type of hymnal cadence. I thought I knew what this was but I was mistaken. I had it mixed up with “evoe”, which is the frenzied cry of the maenads (from Greek εὐοῖ). I first encountered this word in Zelazny's Doorways in the Sand, of all places. The protagonist is at a bacchanal party, also attended by the requisite donkey, and:
A sleepy-eyed girl seated near the hanging beads suddenly sprang to her feet, tearing at her hair and blouse buttons, crying, "Evoe! Evoe!" the while.
The girl does not appear again, but the donkey is a plot point. If there is a canonical name for Silenus’ donkey, I do not know it.
Similar but not related is “ululation”, which is just what it sounds like, a long wavering howl. This onomatopoeic word is very old. It is not, however, related to uvula, which is Latin for “little grape”.
To me “ululate” suggests that there ought also to be “ululatrix” and perhaps also “ululatorium”. If I wrote a novel it would be full of this sort of nonsense.
“Shock: Some Jersey Shore boardwalk games are fixed, inspectors say”
Ground penetrating radars use radio signals that are capable of penetrating into the ground…
(“Underground Lake Found On Mars Beneath A Mile of Ice”)
The thing about technical experts in filth reminded me of something I've wondered for a long time.
Form 1040 (which is the principal individual tax reporting form in the U.S.) has a space at the bottom for “Your occupation”. I usually fill in “computer programmer”.
But what does Alex Rodriguez put there? Does he write “shortstop”? (Or, now, “retired shortstop”?) Or something less specific?
If I were a shortstop, I would definitely want to hand out business cards that said “shortstop”.
Last year someone asked an interesting but off-topic question on math stackexchange:
How voltage drop occurs in a resistor?
So I was getting confused over a thought, say I have a resistor and we have 10V source across it, now when electrons flow from negative end to the positive end they lose 10 joules of energy as they flow through the resistor, now with all the weird and crazy quantum stuff happening inside the wires how can we exactly predict how much energy an electron is going to lose that precise amount of energy when it passes through the resistor, can’t it do this - lose 5J of energy inside the resistor and continue with 5J energy left ?
Well, that is a good question, and I didn't really know the answer because I know very little about physics. But I thought about it and thought maybe I had the explanation, so I replied in the comments.
The question was later deleted, but I saw it again recently and thought that my explanation was worth preserving, so here it is:
I think the answer is going to look like this: if you throw a handful of fine sand, all the grains identical, off of a 100m cliff, some grains might fall straight down, some might be caught by the wind and whirled all about, but every single one will lose exactly !!100g/m!! joules per kilogram, where !!g!! is the acceleration of gravity in meters per second squared and !!m!! is the mass of a grain.
Three hours later:
Considering this more, I think the analogy is pretty good. The 10J loss (actually 10eV, but the principle is the same) is not a property of the resistor but of the power source. You can replace the resistor with any other resistor — bigger, smaller, different shape, different material, whatever — and the energy loss per electron will not change. The electrons lose 10eV each because the power source is a 10V source. This does not mean that it imparts 10eV to each electron; it means that the energy difference between its two terminals is 10eV per electron. The energy measurement is relative.
“Per electron” in the next-to-last sentence is wrong, but I think the rest of it is pretty good. In particular, my point about how the energy loss is not a property of the resistor. The energy loss is the same, regardless of the resistance; this is Kirchoff's voltage law. If you replace the resistor with one of lower resistance, the energy drop through it is still exactly the same (per electron), but the voltage source is able to push electrons through it at a greater rate; this is Ohm's law.
According to the U.S. Food and Drug Administration's Defect Levels Handbook:
In this procedure, FDA's technical and regulatory experts in filth and extraneous materials use a variety of criteria, often in combination, in determining the significance and regulatory impact of the findings.
Now I want business cards that say “technical expert in filth and extraneous materials”.
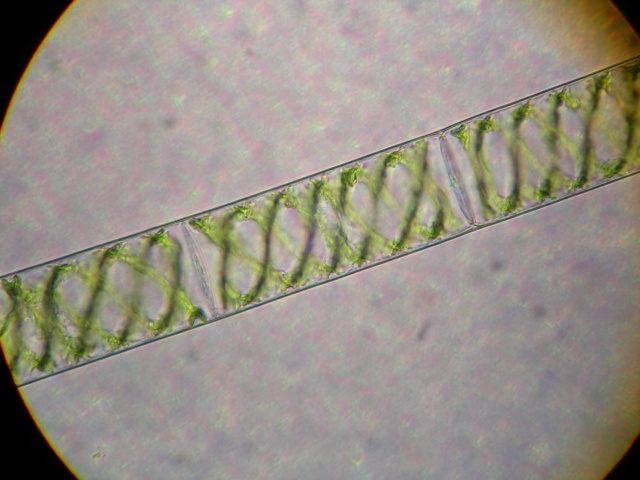
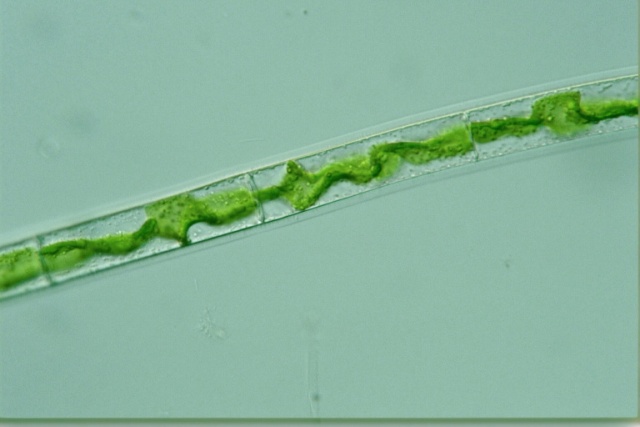
There are several similar-looking species of yucky pond-infesting green algae that can only be distinguished with a microscope.
Spirogyra can be recognized because its chloroplasts are arranged in helices:
But Zygnema has star-shaped chloroplasts:
And Mougeotia has ribbon shapes:
To the the naked eye they all look like slimy green mats.
This is on my mind because over the weekend Toph and I camped in Parvin State Park, which boasts a swimming area in their lake. The swimming was not good, in large part because the lake is filled with slimy green mats.
The Protist Information Server at Hosei University is the source of the Mougeotia image above, and has many additional images of all sorts of yucky green slime. The Spirogyra image and Zygnema image are from Wikimedia Commons; Zygnema is by Bob Blalock of English Wikipedia.
This field guide to scum, by M.S. Kannan and N. Lenca of Northern Kentucky University, was comprehensive and interesting.
Mozart wrote a canon titled Leck mich im Arsch, which means what you think it does.
Also, the Wikipedia article about this begins with the hatnote:
For the Insane Clown Posse recording, see Leck mich im Arsch (Insane Clown Posse song).
which is not something I expected to see.
Estimating quanities like !!\log_2 3!! is easier than it looks, if you know a couple of tricks. In the previous article I said:
I estimated that as 1.6 off the top of my head just by half-assing it: !!2^{3/2} \approx 2.828!!, so it must be a little bigger than !!\frac32!!, which it is.
I really did do it in this ridiculous way, starting from !!1.5 \Rightarrow 2.828!! and then adding a fudge factor to get !!1.6 \stackrel?\Rightarrow 3!!.
(The !!2.828!! is because !!2^{3/2} = 2^{1/2}\cdot 2 \approx 1.414 \cdot 2 = 2.828!!, and memorizing !!\sqrt2\approx 1.414!! is something everyone does in high school.)
I could have arrived at the same answer by a slightly less fudge-flavored route: $$\begin{align} 256 = 2^8 & \approx 3^5 = 243\\ 8\log 2 & \approx 5 \log 3 \\ \frac85 & \approx \frac{\log3}{\log2} = \log_2 3. \end{align} $$
Using a slightly less cruddy initial approximation, !!2048 = 2^{11}\approx 3^7 = 2187!!, we get !!\log_2 3 \approx \frac{11}7 = 1.5714\ldots!!. The correct value is !!1.58496\ldots!!. Incidentally the computer informs me that !!524288 = 2^{19} \approx 3^{12} = 531441!!, yielding the approximation !!\frac{19}{12} = 1.5833\ldots!!, but I did not know either of those off the top of my head. I only know the powers of !!3!! up to !!3^7!!, or maybe !!3^8!! on a good day.
We can similarly notice that !!125 = 5^3 \approx 2^7 = 128!! and so estimate that !!\log_2 5 \approx \frac 73!!; the correct value is !!2.322\ldots!!.
File this under “lower mathematics”.
I spent some time over the last couple of days trying to estimate the number of smooth numbers up to !!N!!. (An !!n!!-smooth number is one whose largest prime factor is no larger than !!n!!. So the 2-smooth numbers are exactly the powers of 2, and the set of 3-smooth numbers contains exactly the numbers of the form !!2^i3^j!! and begins !!1, 2, 3, 4, 6, 8, 9, 12, 16, 18…!!.)
Let's write !!f_k(n)!! for the number of !!k!!-smooth numbers up to !!n!!, so for example !!f_3(19) = 10!! and !!f_2(19) = 5!!, as above. Then obviously !!f_2(n) = 1+\lfloor \log_2 n\rfloor!! exactly.
(Incidentally, I think there ought to be a simpler notation for !!\lfloor \log_k n\rfloor!!, which comes up really often.)
After hacking around a bit, I settled on $$f_3(n) \approx \ell_3(n) \cdot f_2(n) - \frac{\ell_3(n)-1}{2} \left( \ell_3(n)\log_2 3 - \frac12 \right) $$
where !!\ell_3(n) = \lceil \log_3 n\rceil!!. I expect I can express !!f_5(n)!! in terms of !!f_3(n)!! in similar fashion but haven't yet tried. The may still contain some silly errors (I corrected a bunch), but at least the computer says it is not too far off. For example the approximation guesses !!f_3(10^6) \approx 139.4!! and the correct answer is !!142!!.
I wanted something I could compute in the woods with no calculator, because Toph and I went camping this weekend and I had my phone off and didn't want to turn it on. I think the formula above answers the requirement pretty well. Note that calculating !!\ell_3!! exactly is quite easy, much easier than calculating !!\log_3 n!!. The only possibly tricky bit is the !!\log_2 3!!, which I should have memorized but don't. But in the woods I estimated that as 1.6 off the top of my head just by half-assing it: !!2^{3/2} \approx 2.828!!, so it must be a little bigger than !!\frac32!!, which it is.
This formula comes without absolutely no warranty, not even the implied warranty of merchantability or fitness for a particular purpose.
I remember we used to make jokes that went something like “What's the scariest thing you'll find wandering the halls of the engineering school? A programmer with a screwdriver.”
But we were wrong. A programmer with a screwdriver can only do so much damage. To really fuck things up, a programmer needs a keyboard.
Years and years ago I gave a tutorial the the Perl Conference called Tricks of the Wizards. (I should really make that publically available. Someone please remind me later.) In this talk I was careful to explain that I was not, myself, a wizard; I was only presenting the tricks of the wizards. Wizards canonically wear large pointy hats with astonomical figures on them. Lorrie made me a small hat with astronomical figures.

But a few years later at YAPC, Larry Wall gave a keynote in which he analogized different members of the Perl community to characters in Lord of the Rings, and admonished us to not underestimate the hobbits. Talking to Larry afterwards, he remarked that I was one of their best elves.
“Really?” I said. “I think of myself as clearly a dwarf, crafty and irritable, toiling alone in my underground cavern, forging marvelous jewels for myself and magical tools for other people to use.”
Then Larry paid me a compliment I will treasure my whole life. He said that I was a wizard, because the role of wizards is to be able to get separate groups to work together, by virtue of not being part any group themselves.
Well then! If Larry Wall said I was a wizard, I was a wizard. I eliminated the disclaimer from my talk, and I asked Lorrie to make me a full-sized hat:

She also made one for Placido the octopus, who accompanies me to all my conference talks.