Mark Dominus (陶敏修)
mjd@plover.com
I have another blog that doesn't suck.
Archive:
| 2023 | JF |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFM |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | ND |
Comments disabled
git-commit-tree won't create a merge commit where two of the parents
are identical.
% echo Planarian power | git commit-tree HEAD^{tree} -p HEAD -p HEAD
error: duplicate parent 3627118bf5d5e1af75a10f640c1aee9c397d257e ignored
9f41d9f782ff9800558f8317840d0dab3ee961cc
% git log -1 --pretty=%p 9f41d9f782ff9800558f8317840d0dab3ee961cc
3627118
Darn it, Git, I wanted to shoot my foot off!
Mark Dominus: I ordered two pairs of headphones. Your package arrived today. Only one pair of headphones was in it. On your web site, you claim I only ordered the one pair. But you still charged my credit card for both pairs.
Denise W.: Ok. May I please know when the amount was charged with this credit card?
Mark Dominus: 02/24/18 Transaction number S6NeTk7zXVoFx29T3.
Denise W.: Upon checking, I didn't locate any related order with all the information you posted. May I please know have you checked with your credit card bank*
Mark Dominus: No, I learned that 17-character alphanumeric transaction ID from my magical friends in the the spirit world.
Many people have observed that French is much more verbose than English, at least it is currently. I wasn't thinking about it then, but yesterday's Darth Vader joke was (perhaps? maybe not) an interesting example. When I translated it to English, I cut it from 17 words to 11. The current fashion in English-language humor is to trim the setup to the bone.
It was not always so. Here is a highly typical example from Joe Miller's Jests, originally published in 1739:
On the Duke of York's horse Moses winning a match at Ascot, his royal highness appeared to look very thoughtful. A spectator asked Mr. Hunt, who happened to be present, what he supposed the royal sportsman could then be pondering on? ‘Why, you know,’, replied Mr. H. ‘that the duke is a bishop, and he is doubtless thinking of Moses and the profits.’
The useful word of the day is “imbricated”, which means overlapping in the manner of roof tiles or fish scales. You're welcome.


| |
| Imbrications | |
For further investigation: what exactly does an imbricatrix do? Why?
(Picture credits: scales: Rajesh dangi at English Wikipedia; tiles: Biswarup Ganguly.)
My kids left for school this morning, and just before the front door closed I heard Toph exclaim “what use is finding the area under a curve?!?!”
I don't know what the hell that was about, but I jumped up, opened the door again, and proclaimed:
“Finding the area under a curve is one of the central problems of calculus, which is one of the great achievements of the human mind, and is essential for physics, architecture, and engineering.”
“Oh,” said Toph. “Well, okay then.”
I said I only knew three. But thanks to Dave Long, I now know four! And the new one is in French! (Translation is mine.)
Dark Vador va à la boulangerie. Qu'est-ce qu'il commande ? 3 petit pains et 2 tartes tatin. Pourquoi ?
(Darth Vader goes to a French bakery. What does he order?)
PAIN ... PAIN ... PAIN ... TARTE TATIN! TARTE TATIN!
Thank you, M. Long!
Just about three years ago, in an article about contracts I had refused to sign, I wrote:
[Comcast's] proposed agreement included a clause in which we promised not to buy Internet service from any other company for the next ten years. I refused to sign. The guy on our side who was negotiating the agreement was annoyed with me. “Do you think you're going to get FIOS in here in the next ten years?” he asked sarcastically.
For the record: We got FIOS in here last month.
It's been tough for anyone to wear a mustache since that asshole in Germany ruined it, but some people manage to pull it off. A while back I asked for examples of post-Hitler wearers of noteworthy mustaches. (It's not enough to be a noteworthy person who happens to have a mustache; the mustache itself must be noteworthy.)
Burt Reynolds and Tom Selleck stand out here. Rollie Fingers comes to mind. Freddie Mercury, John Waters, Geraldo Rivera, and surely there are many others. (Chaplin and Dalí don't count: too early. Clark Gable is borderline.)
The toothbrush mustache, though, is dead. Even Michael Jordan could not rehabilitate it. He wore one in a 2010 Hanes commercial and was universally condemned. Charles Barkley spoke for everyone:
I don’t know what the hell he was thinking.
I find it surprising that there is more than one joke of the following type, but here are three:
Q: What is Batman's full name?
A: Nananananananananananananananana BATMAN!
Q: What did the Pink Panther say when he stepped on an ant?
A: Dead ant. Dead ant. Dead ant dead ant dead ant...
Q: Where does the Lone Ranger take his trash?
A: To the dump, to the dump, to the dump dump dump…
[ Addendum: Dave Long sent me another! ]
I'm so old, I can remember the brief period during which the phrase “politically correct” was used without either irony or derision.
This is going to be sort of vague. This morning I was thinking about what the Perfect Octopus would be like, but I don't think there really is such a thing. Obviously it must have eight arms, but merely having eight arms is not sufficient for a thing to be an octopus (or even necessary) and octopuses come in many varieties. There is no one single canonical octopus, to which any entity can be compared to determine its degree of octopus-ness.
There are, though, some properties that are like that. This example is not perfect, but it gets at what I mean: to what degree is an entity Kafkaesque? There is only one way to decide, and that is to compare the entity with the works of Kafka. Opinions may differ about how strong the resemblance is, but the works of Kafka are the standard, and the only standard. Any other proposed standard has authority only by transitivity. And if the works of Kafka aren't themselves Kafkaesque, then nothing is.
In some ways, the International Prototype Kilogram is an extreme example of this: an object has a kilogram of mass if, and only to the degree that, its mass is equal to that of the IPK. But in other ways this is not at all the example I want. My great-uncle's graduation ring is not a kilogram, even though it closely resembles the IPK in being roughly cylindrical, mostly made of platinum and residing in Grenoble.
What I'd like is to find classes of things that are defined by their overall similarity to a single prototype. So far the best example I've thought of is a Hitler mustache. I'd prefer an example that wasn't associated with an individual person, and very much prefer a non-Hitler example.
If you are sending unsolicited email messages that include a phrase to this effect:
Don't want emails from me anymore? Reply to this email with the word "UNSUBSCRIBE" in the subject line.
that means you are a spammer, and you should stop spamming.
If your response to this is “but the people I'm emailing might be very interested in what I have to say” then yes, you are still a spammer; that is what every spammer says and what every spammer has said in the entire history of spamming. And you should stop. You may be fooling yourself, but you are not fooling anyone else.
I wanted to write this article, but the author got there first and did a better job than I would have done anyway, so you should just read it.
Words for “yes” in Romance languages
Usually if I misspell or just mistype a Google search term, it does a remarkably good job of guessing what I really meant. Most of its failures come from overeager guessing in cases where I correctly spelled something that just happens to be spelled strangely.
But today, it flubbed. I asked it to search for “Brigitte Zacharchenko” and it failed to find her, suggesting instead “Brigitte Zakharchenko”.
This actually messed up the one part of the spelling that I had right, and the search failed.
The correct spelling is “Brigette Zacharczenko”.
This afternoon from the Department of “embarrassing stuff we did as kids that we wish everyone would stop bringing up”:
Scorpion and Felix, A Humoristic Novel is the only comedic fictional story to have been written by Karl Marx. Written in 1837 when he was 19 years old, it has remained unpublished. … The surviving fragments of the book's manuscript have not been well regarded. Francis Wheen in his biography of Marx characterizes the work as “a nonsensical torrent of whimsy and persiflage” which was “dashed off in a fit of intoxicated whimsy,” … The novel was never finished. Only some chapters of the novel survive to the modern day. Parts of the novel could have been burned by Marx himself…
“Hello, your guy just delivered my pizza, and it is not what I ordered! I wanted half-pepperoni for me, and half-mushroom for my brother-in-law.”
“I'm very sorry, sir, we'll send over another pizza right away. Can you tell me what kind you got?”
“It was all messed up! My half was like two-thirds mushrooms, and his half was mostly pepperoni.”
I'm so old, I remember attending a meeting the Adobe people held at my workplace to try to convince us to adopt their new “PDF” thing.
The following story appears in George Gamow's memoir My World Line:
Here is a story told to me by one of my friends who was at that time a young professor of physics in Odessa. His name was Igor Tamm (Nobel Prize laureate in Physics, 1958). Once when he arrived in a neighboring village, at that period when Odessa was occupied by the Reds, and was negotiating with a villager as to how many chickens he could get for half a dozen silver spoons, the village was captured by one of the Makhno bands, who were roaming the country, harassing the Reds. Seeing his city clothes (or what was left of them), the capturers brought him to the Ataman, a bearded fellow in a tall black fur hat with machine-gun cartridge ribbons crossed on his broad chest and a couple of hand grenades hanging on the belt.
‘You son-of-a-bitch, you Communist agitator, undermining our Mother Ukraine! The punishment is death.’
‘But no,’ answered Tamm, ‘I am a professor at the University of Odessa and have come here only to get some food.’
‘Rubbish!’ retorted the leader. ‘What kind of professor are you ?’
‘I teach mathematics.’
‘Mathematics?’ said the Ataman. ‘All right! Then give me an estimate of the error one makes by cutting off Maclaurin's series at the !!n!!th term. Do this, and you will go free. Fail, and you will be shot!’
Tamm could not believe his ears, since this problem belongs to a rather special branch of higher mathematics. With a shaking hand, and under the muzzle of the gun, he managed to work out the solution and handed it to the Ataman.
‘Correct!’ said the Ataman. ‘Now I see that you really are a professor. Go home!’
(However, Dam Thanh Son has found and translated a more reliable version of the same story, from the memoirs of Tamm's grandson, L.I. Vernsky.)
Once when I was telling this story to some friends, I got to the part where the Ataman issues his challenge: “‘Calculate the error when the Maclaurin series is truncated at the !!n!!th term… OR DIE!’” This caught the attention of Katara, who was with us, then around fifteen months old. She perked up and proclaimed “AWW DIE!!!”
For the next few weeks she would startle us by interrupting whatever else was going with “AW DIE!”
This is why you need to be careful what you say around an impressionable child.
The following is one of my favorite excerpts; I typed it in and have carried it around for 25 years. It appears on pp.220–221 of Edgar R. Lorch, Szeged in 1934, American Mathematical Monthly, vol. 100, #3, pp.219–230.
All of us Fellows were terrified what would happen to us if we couldn't locate a spot for next year. At this time the political super-potentates of the mathematical scene were centered in Princeton, N.J., where the Institute of Advanced Study had recently been established. The School of Mathematics was its leading school. There were about five mathematics professors at the Institute. In order to further distinguish them from ordinary mortals teaching at Columbia, Yale, or other universities, each professor had an assistant. There was tremendous variation in the duties of these assistants. It was traditional belief that Einstein's assistant did nothing. The only requirement for him was to be a Jewish exile from Nazi Germany. Hermann Weyl's assistant had normal duties: preparing in mimeographed form his professor's lectures on group theory. I cannot imagine what Alexander's or Veblen's assistants did — probably not much.
In early spring these potentates got together, counted up the mathematical plums to be handed out for the year, and made a list of the available talent who constituted the target space on which these plums were to be mapped. Then they sent the customary letters to the candidates: a three-paragraph personal letter to the candidates who had been hit, and a one-paragraph note of non-success to the poor souls who did not make it. One day I learned that one of my friends had received his letter — a good one. I gingerly went home, and sure enough, there was a letter from the Institute. The type-print covered the whole page — success! I would be able to live another year.
The letter was really exciting. I was being offered the job of assistant to John von Neumann! I had heard him lecture several times. He was brilliant, spoke very fast, his English was quite fluent, he made remarkably few errors.
I made a trip to Princeton and met with Veblen, who was running the Institute. “What,” asked I, “are the duties of an assistant to Professor von Neumann?” Veblen answered with a mixture of surprise and disdain, that a mere private second class should ask such a question about a four star general. His answer staggered me. Here were the four principal duties of von Neumann's assistant:
To attend von Neumann's lectures on operator theory on Mondays, Tuesdays, and Wednesdays, take copious notes, complete unfinished proofs, see them through the secretarial jungle, and promptly circulate them to all American university libraries. This task alone was consuming the entire energies of a younger person, who had to be very sharp, fast, clever, and tough. These notes ran to over 600 pages.
To be von Neumann's assistant as Editor of the Annals of Mathematics. This meant reading through every manuscript accepted for publication, underlining Greek letters in red and German letters in green, and circling italics. Also writing in the margins all necessary instructions to printers. The following anecdote illustrates the hazards of being editorial assistant of the Annals in the early thirties. A manuscript was submitted by the brilliant Soviet mathematician, Lev Pontryagin. Since paper was then exceptionally scarce in the Soviet Union, Pontryagin had taken wrapping paper, torn it into appropriate-sized pieces, and gone to work on his typewriter. Unfortunately, Pontryagin was blind. The wrapping paper was torn unevenly, and a good portion of the words and symbols in the margins were missing. No matter. The Annals editorial assistant retyped the paper, supplying all the missing symbols. What a hero!
To go once a week to the printers of the Annals of Mathematics in Baltimore in order to instruct them in the art of typesetting mathematical symbols with subscripts, superscripts, subsubscripts, etc. The Annals of Mathematics had been printed in Hamburg, Germany by the firm of Lutke and Wolk. In view of increasing anti-Semitism under Hitler, the German connection was given up in favor of printing in the United States. But no American printer had ever before set up mathematical symbols! They were complete illiterates. Solution: Let von Neumann's assistant teach them!
To translate into English von Neumann's numerous 100-page papers. Now that von Neumann was a professor in an American institute, it was thought that his papers should appear in English, not German. Since von Neumann was provided with an assistant, it was natural that the assistant should do this.
You may recall that this was extracted from an article titled Szeged in 1934.
That is because the author, Lorch, decided that he was not cut out for the job, and fled to Hungary.
Countability of Fibonacci series asks:
How is the countability of Fibonacci sequence proven?
Somewhere along the line I mistyped “reservoir” as reservoid, which seems like a fortunate coinage. I'm not sure just what reservoids are, but I imagine some sort of extradimensional storage space. Perhaps in the Harry Potter world it's a trademark for a Bag of Holding? Except no, in that world they have an Undetectable Extension Charm and anyone can cast it, say on a horn filled with seawater.
Google search produces a mix of obvious typos and interesting leads that, on investigation, turn out to be typos. For example, the top hit is about special firewood-storage shelves for next to your fireplace, whose name is actually the totally unimaginative “reservoirs”. A reference to Quentin Tarantino's lost masterpiece Reservoid Dogs is similarly a simple error.
Hit #6 is the Wikipedia article for reservoir sampling, which I took as Google just being a its creepy stalker self.
Hit #8 is from a 1912 Kentucky regulation about slaughterhouse construction.
I also tried searching the database of U.S. trademarks; nobody has trademarked “reservoid”. The term is wide open for anyone who wants to use it.
Regarding my recent discussion of algorithms to select exactly half the items from a finite but unbounded stream: Although I am persuaded by the argument I gave that there is no algorithm better than loading the whole thing into a buffer first, I still find this quite counterintuitive and I feel that if there is tnot some wrinkle that none of us have appreciated yet, then my intuition here is in need of a significant correction.
In the original problem, we had a stream of !!2N!! items, but we didn't know what !!N!! was. We were required to select exactly !!N!! of them for output, with each possible subset appearing with probability !!{2N\choose N}^{-1}!!. The question was essentially “is there a method for doing this that requires less memory than just sucking the whole stream into a buffer”, and the answer was “no”.
Let's take what appears to be a much easier version of the same problem. First, instead of requiring the outputs be equiprobable, we will only require that each possible output set appear with some positive probability.
Let's also say that instead of selecting exactly half the items, we are only required to select !!\lfloor\log_{10} N\rfloor!! of them. (We can even constrain things further by requring !!N!! to be a power of 10, but I don't think it makes a difference.) So:
We are only required to emit !!\lfloor\log_{10} N\rfloor!! of the !!N!! inputs, say if there are ten billion we only need to select and emit ten.
We are not required to select the possible outputs with any particular probability, as long as there is some possibility of producing each possible selection.
The only memory constraint is that we are not allowed to read the entire input into a buffer in every case. There must be some !!N!! for which, when the input contains !!N!! items, we have a chance of using at most !!N-1!! memory.
It seems incredible to me that there is no way to solve this problem, but I think that is so.
One possible strategy is to start producing output before reading all the input. I am pretty confident that this can never work. Say that after reading the first !!k!! items, we emit some item !!R!!. We have foreclosed the possibility of producing an output that omits !!R!!, but that itself is no problem, as long as we don't do it every time. The real problem is: we have also foreclosed the possibility of producing an output that omits all of the first !!k!! items, and that has been foreclosed every time. If the input contains fewer than !!10^k!! items we can escape detection, but if it has more than that we have screwed the pooch. So it can never work to emit items before reading the end of the stream.
Now say we have just read the first item. We can store it, emit it, or discard it. Emitting it immediately would be a failure, as I just discussed. And discarding it is also a failure, because if we discard it immediately we might later discover that !!N\ge 10!!, and that we were required to have a positive probability of emitting item 1. So we must store it, at least temporarily.
Now we read the second item. Again, emitting it and discarding it are losers, for the same reasons as before. Emitting 1 now is just as bad is doing it before would have been. Overwriting item 1 with item 2 is a little better, as long as we do it stochastically. (This is what makes ordinary reservoir sampling work.) But it forecloses the possibility of emitting both 1 and 2, and if !!N\ge100!! we are required to have had a chance of doing that. So the only remaining choice is to store 2 along with 1.
Say we have stored the first 9 items, and we have just read the 10th. Now the situation is a little different. We know, for the first time, that that output must include at least one item. But we still can't select one of these ten items to emit immediately, for the same reasons as before: an algorithm that does that has zero chance to emit, say, just !!\{s_{43}, s_{57}\}!!, which it is required to do with positive probability if !!N=100!!. And we can't select an item and discard it, because an algorithm that does that has zero chance to emit exactly !!\{s_1, \ldots s_{10}\}!!, which it is required to do with positive probability if !!N=10^{10}!!.
How long do we have to hold onto those first ten items? We certainly can't do anything about them until we resolve the question of whether !!N\ge10^{10}!!. If we hit the end of the stream, we know what to do, but the whole point was to not hold onto them until we got all the way to the end. And the situation isn't any better once we get out to the !!10^{10}!!th item, just as the situation with item 1 was no better once we got to the 10th item. We have to store all of the first !!10^{10}!! items, against the possibility that the input might contain at least !!10^{10^{10}}!! items so that our output has a chance to contain all of the first !!10^{10}!!.
If we are required to select, say, one million items from an unbounded stream, we can do it with a constant amount of memory, regardless of the size of the stream. But if we are required to select !!\frac N2!! or !!\sqrt N!! or !!\log N!! items, even if that is a tiny tiny fraction of the whole, even an inverse Ackermann function or something, there is no way to do it without storing the entire stream in an array. I am amazed.
A couple days ago I observed that although Tom Waits was born in 1949, well into the color film era (Kodachrome was introduced in 1935), almost all the available photographs of him are in black and white, which I think tells us something interesting about Tom Waits, although I'm not sure I could say exactly what. I wondered who else might have this attribute.
Craig Burley has found another example: William S. Burroughs. Although he was born in 1914, he lived until 1997 and you would think there would be many color photographs of him. But most are black and white. For example, Wikipedia's portrait is B&W even though it was taken in 1977.
Abigail has presented a convincing argument that the sampling algorithm I asked for does not exist.
Suppose the algorithm has read the first !!N!! items. It does not yet know how many there will be in all; there might be !!2N!!. But if there are !!2N!!, there is a positive probability that the !!N!! it has read are exactly the !!N!! it will emit, and the only way it can do this is if it has retained all !!N!! in memory.
But if it has retained all !!N!! in memory, and then discovers that there are no more to read, it has exceeded the memory bounds. (Or rather, it must since the argument is the same for all !!N!!.)
This rules out not only a sublinear memory bound, but any result that would use less memory than reading all the items into a buffer.
Here's yet another variation on reservoir sampling that I haven't seen before.
You have a stream that will produce !!2N!! items, one at a time as they are requested, but you don't know ahead of time what !!N!! is. You want to select exactly !!N!! of them at random, and you want each of the !! 2N\choose N!! possible subsets chosen equiprobably.
But you must do this with exactly !!N + O(1)!! memory. (Doing it with !!O(N)!! memory is easy: just suck the whole stream into a buffer.) Is this possible? I'm really not sure. If not, is it possible with !!N + O(f(N))!! for any sublinear !!f(N)!!?
If it is possible, probably it is not hard to generalize the method to selecting !!N!! of !!kN!! items for any positive !!k!!.
[ Thanks to Dfan Schmidt for pointing out that I did not originally ask for what I wanted. ]
[ Answer: Nope. ]
Last week sometime I had an interesting idea for a variation on reservoir sampling that I'd never seen before. Then I forgot about it. Yesterday I remembered for the first time that I'd had this idea, and I was frustrated that I couldn't remember what it was. I racked my brain all evening and the following morning trying to remember it, and today I did remember, shortly before noon.
I stopped in my tracks and pulled out my phone to make a note. I
typed in weigh and it offered to autocomplete to weighted, so I
accepted. Then it offered the next word: reservoir, and sure
enough, the next autocompletion was sampling.
So I must have made a note about it already, and I was going to end this article by pointing out that I had had it on my to-do list since last week, sheesh, and all my brain-racking was for nothing. But then when I looked for it, it wasn't there. So I think I must have recorded it somewhere, but I can't find the record. I don't know if that's better or worse.
Actually it occurs to me now that maybe I didn't make a record before, and that my phone knows about it because I did a Google search for it shortly after getting the idea. In that case the brain-racking was justified, I would be pretty much off the hook for everything, except the basic omission of forgetting to make a note of it in the first place.
I'll write up the weighted reservoir sampling thing sooner or later, probably on the Universe of Discourse.
So I did Google image search for Tom Waits, and the results are striking:
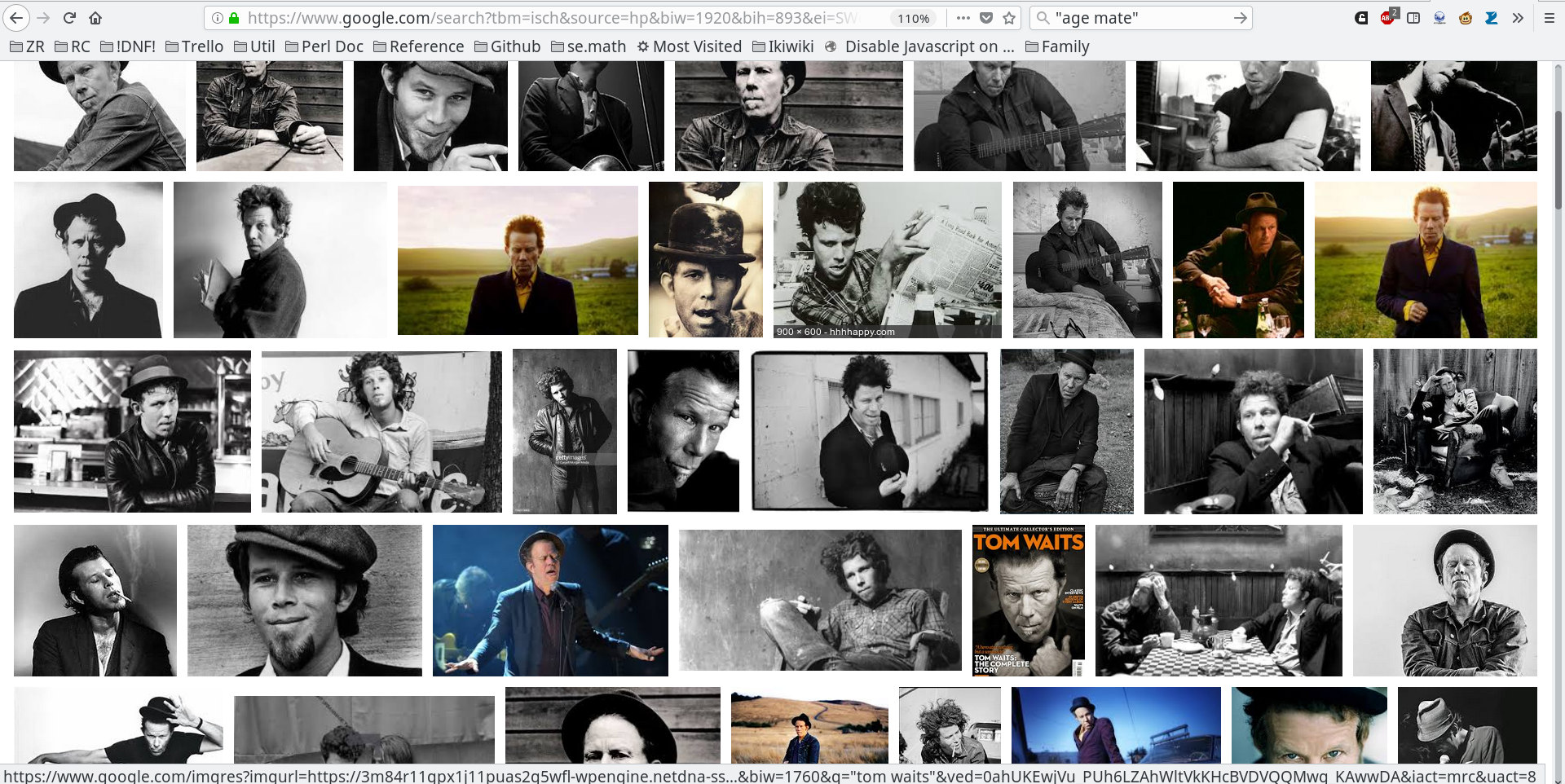
General opinion is overwhelmingly against the idea of color photographs of Tom Waits.
I tried to think who else might be like this. The only person I thought of was William Kennedy, but the effect wasn't nearly as pronounced. I'll sleep on it.
[ Craig Burley points out that William S. Burroughs also has this distinction. ]
I was looking at yesterday's article on my phone. In horizontal orientation the illustration looked fine:
But in vertical orientation the browser (Firefox 58.0.1) rendered the two SVG images at completely different scales:
I think the two page elements are identical and that the two SVG files have the same natural size, the same scale, etc. Does anyone have any idea why this happened? Is it something I did? Is it something I could prevent?
[ Addendum 20180212: The mystery has been solved; I'll post it here later this week. ]
I have been thinking for a long time about the way mathematicians use terms like “obvious”, “straightforward”, “trivial”, and so forth, and the different shades of meaning these communicate. Someday I will publish a longer and more complete discussion.
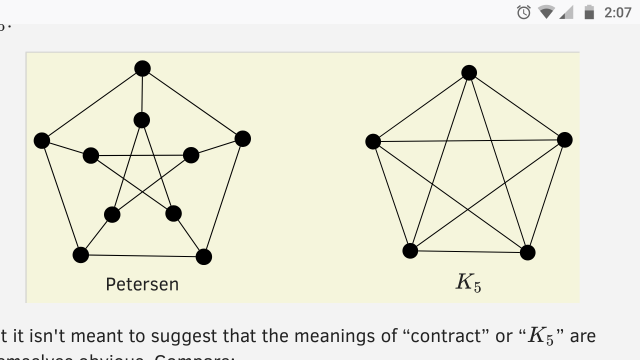
Meantime, here's a thought. Discussing the Petersen graph recently, I said:
The standard presentation, above, demonstrates that the Petersen graph is nonplanar, since it obviously contracts to !!K_5!!.
To someone not versed in graph theory, this not only isn't obvious, it's unintelligible. In fact, it's indistinguishable from a meaningless parody:
The Cosell configuration, shown above, is semispatulated, since it obviously extends to a !!\zeta!!-complete net.
But I also think this is an exactly correct use of “obvious”:
I said it obviously contracts to !!K_5!!. If you know what a contraction is, and what !!K_5!! is, this is obvious. In fact the first thing you might notice, if you were seeing the Petersen graph for the first time, is how much it resembles !!K_5!!:
Petersen !!K_5!! But it isn't meant to suggest that the meanings of “contract” or “!!K_5!!” are themselves obvious. Compare:
Obviously, a fly ball that leaves the field ouside of fair territory is never a home run.
If you don't know at least the approximate definitions of the technical terms there, you will be in the dark. But that doesn't make this an inappropriate application of the term “obvious”.
The Petersen graph also contracts to !!K_{3,3}!!, but I doubt anyone would say that it was obvious, at least not from seeing this presentation.
I didn't say that the graph was obviously nonplanar. The contractibility is obvious, but the nonplanarity follows from that by Kuratowski's theorem, which nobody claims is obvious. (Quite the opposite!)
Contrast this with:
The Petersen graph is nonplanar, since it *trivially contracts to !!K_5!!.
I think “trivially” here is wrong, and people might object. That would suggest that no actual contractions need to occur. !!K_5!! trivially contracts to !!K_5!!, but the Petersen graph does not.
- To prevent possible memory exhaustion, be sure to clear the cache after every request.
Vernor Vinge likes to use “Q” to represent the /t͡ʃ/ sound of English “church”, similar to how it is used in pinyin. But he does this even in places that Chinese does not. So for example, there is an organization in some of his novels called the Qeng Ho, pronounced “cheng ho”, and inspired by the historical Chinese mariner Cheng Ho. But Cheng Ho is not romanized with a “Q”; in Pinyin it is written “Zheng He”.
In the case of the Qeng Ho this is totally legit, because the Qeng Ho exist ten or twenty thousand years in our future, and Vinge can make up whatever language he wants for them. He does like to hint that the languages in those novels are descended from Earth languages, but in ten thousand years anything can change.
However! One of the main characters in his 1986 novel Marooned in Realtime is Marta Korolev, and her full name is given at one point as Marta Qih-hui Qen Korolev. I now wonder if Vinge was thinking of the extremely common name “Chen” (陳) when he named Marta Korolev “Qen”.
But “Chen” is not spelled with a Q in Pinyin. It is spelled “Chen”. Not only is there is no name “Qen”, but there cannot be because in in Mandarin “q” is never followed by “e”. And Korolev was born around the beginning of the 21st century, not 10,000 years from now.
Oh well. Maybe “Qen” is Albanian.
In 2001, I noticed something fun. One of the main characters in Vernor Vinge's 1999 novel A Deepness in the Sky is Qiwi Lin Lisolet. One of the main characters in his 1986 novel Marooned in Realtime is Marta Korolev, and her full name is given at one point as Marta Qih-hui Qen Korolev. Aha, they have the same name — “Qiwi” appears to be a modified spelling of “Qih-hui”.
I emailed Vinge about this:
Does the name have some special meaning?
He replied “Wow!”
Vinge told me that although they did indeed have the same name, and he did intend “Qiwi” to have been be descended from the real Chinese name “Qih-hui”, his repeated use of the name was an unintended coincidence, and he hadn't been aware that he had done it until I pointed it out.
What is the difference between:
- The tree only has depth 2
- The tree has only depth 2
- The tree has depth only 2
??
Lately I have been enjoying the special punctuation mark “!!1!”. I think it is like a regular exclamation mark, except that it expresses a sort of unrestrained exuberance and enthusiasm, but with a strong mocking or ironic connotation.
Too many mathematicians have the same name. This is a problem!
For example, I am always mixing up Garrett Birkhoff and George David Birkhoff. But they at least have an excuse for their similar names: George David was Garrett's father, or maybe his son. One or the other, anyway.
I remember discovering with surprise that Aviezri Fraenkel was not the namesake of Zermelo-Fraenkel set theory. That was Abraham Fraenkel. At least I picked up pretty quickly that Michael Guy was the son of Richard K. Guy. But I once met Andrew Appel and struggled for half an hour to figure out why I had heard of him before, eventually realizing that I had been thinking of his father, Kenneth Appel, who was famous for his proof (with Wolfgang Haken) of the four-color theorem.
In researching this article, I discovered for the first time that noted topologist E.H. Moore, co-inventor of the important net concept and the associated notion of Moore-Smith convergence, is not only not the same person as, but not even related to, noted topologist R.L. Moore.
I am not even going to get into the matter of the dozen or so famous scientists and mathematicians named Bernoulli.
I am happy to admit that most of these are just my own ignorance and carelessness. The Birkhoffs are related. The Bernoullis are related. The names “Moore” and “Fraenkel” are common. My occasional confusion of John Milnor and Robin Milner is inexcusable since they are not even spelled the same way. For a long time I inexplicably conflated professor Scott Weinstein with Dana Scott.
But, Gentle Readers, there is one mistake that I refuse to be responsible for, because the universe has conspired against me. There is a famous graph theorist, the namesake of the Rado graph, Rado's theorem of Ramsey theory, the Erdős-Rado theorem, and other similar matters. As you might expect of a frequent collaborator of Erdős, he is a Hungarian. Obviously, I refer to noted Hungarian mathematician Tibor Radó.
Except no, I don't. Tibor Radó is not known for any of those combinatoric and graph-theoretic results. He is the famous namesake of theorems, but in the wholly unrelated fields of complex analysis and harmonic functions. He never collaborated with Erdős.
The Rado who collaborated with Erdős was noted German mathematician Richard Rado.
A couple of days ago I posted a set of pictures I had taken of property damage near my office, perpetrated by Philadelphia Eagles fans celebrating the Eagles' recent Super Bowl victory.
I now think my response was excessively sour. None of the pictures I took were of intentional vandalism. They were all incidental damage caused by exuberant fans climbing stuff. Not something to be proud of, but climbing for the joy of climbing is not the same as smashing for the joy of smashing.
There were some real instances of lawless vandalism: a car was overturned, one of the display windows at Macy's was smashed, and a gas station mini-mart was looted. But the pictures I took were of a rather different thing.
The Philadelphia Inquirer reported on exaggeration of the disorder in the world press.
A while back I got my ear cartilage pierced. A few people, including my kids, asked if it hurt. I said “you know how it feels when you stub your toe really hard?”
“Yeah?”
“It was nothing like that bad.”
Toph and I were discussing the Pythagorean theorem, and I asked her what the square root of five was. She wasn't sure, but said “two, with a remainder one?”
I think this is an insightful answer. She is correctly analogizing the operation with integer division. In division, we say that !!a!! divided by !!b!! has a remainder of !!r!! when $$a = bq+r\qquad(0\le r \lt b).$$ If we require the condition on !!r!!, the solution to the equation is unique.
The analogous situation for square roots is that the square root of !!n!! has a remainder of !!r!! when $$n = c^2 + r\qquad(0\le r\lt 2c+1).$$ Again, the condition on !!r!! guarantees a unique solution.
The world is full of things that aren't important enough to have their own name. What I find interesting about this is that I think it is important enough to have a name. In connection with square roots we often need discuss the remainder, but we don't call it that.
(I was going to dig up evidence of this, then lost interest and filed
the article in the “publish someday, maybe” folder. But then I
remembered: Content-Type: text/shitpost doesn't need evidence!
Victory!!)
[ Addendum 20180207: a little more context. ]
I got a bunch of upvotes this week for garbage posts, but none for my favorite post. OP presented an ugly cubic graph with ten vertices:
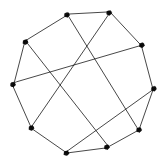
OP asked if this ugly graph was isomorphic to the Petersen graph:
Often the answer to this sort of question is “poke around until you find some ad hoc property that one graph has but not the other. Usually you start by counting up the vertex degrees, which must match. In this case, both graphs are cubic, so that doesn't help. Someone else tried the next thing and found that the ugly graph has a 4-cycle, which the Petersen graph does not, question answered.
But my answer was more elegant. The Petersen graph has many interesting properties. Among other things, it is the smallest non-hamiltonian cubic graph. But the ugly graph obviously has a hamiltonian cycle —the ring around the outside — so it's not the Petersen graph.
This is about the brilliance (and indulgent magnanimity) of Andy Lee. I don't want to steal M. Lee's spotlight by prepending a long and tedious explanation, so I'm going to put the good part up front. Andy Lee sent me this:
Higgledy-piggledy
Mark Jason Dominus
Scrambled some spellings and
Thus made me laugh.Now on a similar
Juxtapositional
Theme he treats friendships as
Paths on a graph.
Wow, my own poem! OK, you can stop reading here.
Wat
This is a verse form called a “higgledy piggledy”.
A while back when I was discussing the anagram “megachiropteran / cinematographer”, Mike Morton (“Mr. Machine Tool”) wrote to point out that he had written a higgledy-piggledy about it. I then mentioned it in one of the several articles about anagrams.
This week Andy Lee pointed out Mike Morton's poem to me on Zulip, and simultaneously wrote to Mike to point out my articles. I found out about the latter when Mike forwarded me Andy's email. I went back to Zulip and said:
This message is pointing out that Mr. Machine Tool sent me a message about your message about my blog post.
Now you should send Mr. Machine Tool email mentioning my Zulip message in which I mentioned his message to me that forwarded your message to him about the connection between my blog post and his tweet.
You could also mention that in my reply to your original Zulip message about Mr. Machine Tool's tweet, I directed you to a blog post of mine that refers to the same tweet.
Finally, I note that “Mark Jason Dominus” scans correctly as the first line of a Higgledy-Piggledy, and suggest that you should put all your further messages in this form.
HOPE THIS HELPS!!1!
I didn't think Andy would actually do it, but look what I got.
Wow. I don't deserve this.
Thanks, Andy.
CNS abbreviates “central nervous system”.
Also “chicken noodle soup”.
You should check out Alexandre Muñiz' Puzzle Zapper Blog. Muñiz invents all sorts of attractive and clever puzzles. There is a lot to like about these puzzles even if you don't particularly care for puzzles. They always have some elegant mathematical symmetry and an interesting concept. Puzzle Zapper also has all kinds of things things related to tilings, geometry and combinatorics.
Today's post is about which pentominoes are the most convex. Obviously, the I pentomino is and the others aren't, but how much aren't they? Well, it depends on how you measure. By reasonable method A, it's the U pentomino; by method B it's the X, and by method C it's a tie between F, T, V, X, and Z.
A particular favorite post of mine was the story about how Muñiz went to the Gathering 4 Gardner and confounded them with his seemingly impossible riddles about the Lo Shu magic square:
8 1 6
3 5 7
4 9 2
It's easy to show, and has been known for thousands of years, that this is the only way (not counting rotations and reflections, of course) to arrange the numbers 1–9 in the cells of a 3×3 array so that the numbers in each row, column, and diagonal add up to the same sum, which must be 15. Muñiz arrived at the Gathering and anounced that he had found not one but two new ways, and the story just keeps getting better from there.
My only regret is that his posts are so infrequent. But every time I see there is a new one I smile and exclaim “Ooh, a new Puzzle Zapper!” and rush off to read it.
I was in Santa Monica for business last year, and the strap on my shoulder bag broke. Very annoying! I could order a replacement, but I would have to have it shipped to my home, and that meant I would be without a strap, hand-carrying my heavy bag containing my fragile computer all over town for the rest of the week. Still it could not be helped.
That evening I went online and asked Google where to order a replacement bag strap, and it duly produced a list of suggestions. But one of them was surprising, and much better than I had hoped for. It showed me a price and a picture of a strap that was available at the REI two blocks up the street, and informed me that the REI would be open for another ninety minutes. Wow! Great! Amazingly useful!
I went up the street and bought the strap, happy ending.
After I got home I was enthusing to Katara about how great this was. Much better than suggesting that I mail order it and then wait for delivery. “But I don't understand what they get out of it,” I said. “When you click through to order on line, Google gets a referral fee. But they can't get any referral fee from REI because they don't know that I went in there half an hour later.”
“Yes, they do,” replied Katara.
Oh, shit. They do.
I'm really not sure how I feel about that.
Now I'm stuck on the idea of what might come after “oaken tokens from Hoboken”. Unfortunately.
Here in Philadelphia we have a place called Shamokin Street and that might have been next.
I suppose this street is named after the town of Shamokin, which is not that far from here, around 2½ hours’ drive. The name is from Lenape, and supposedly means “place of eels”.
Many of the really good names around here are Lenape. One of my favorites is Conodoguinet Creek, a tributary of the mighty Susquehanna River. “Conodoguinet” means “a long way with many bends”.
There are also a lot of places around here named “Perkiomen”, which is also Lenape. Some people say it means a place where there are cranberries.
Why can't we just ask the Lenape what it means? I want to look into this, the details are probably interesting. If they don't know, I suppose part of the reason is phonological shift, and that there are no records of what the language was like 300 years ago. Presumably the main cause, both proximally and distally, is cultural upheaval caused by European immigration, but by what specific mechanisms? The language itself might have changed drastically.
Or maybe the answer is: of course we could ask them, but white people don't bother to.
The Nanticoke Leni-Lenape tribe has a monograph about their history available for download. Useful! I will read it.
Hmm, this article has wandered a long way from where it started. Welcome to my brain.
Non compote mentis is pretty silly — it is some sort of pseudo-joke my sleep-befuddled brain makes in the mornings about non compos mentis — but it occurs to me for the first time that the actual Latin plural of non compos mentis is non compotes mentes.
Maybe that will give my brain something extra to do next time I am making compote. Minty compotes, perhaps.
Every morning I get up before my brain does, I shamble downstairs, and start making breakfasts and lunches for the kids. It's important for me to have an automatic routine for this because I seem to be incapable of any kind of independent thought for the first half hour or so. It works fine as long as I'm doing all the same things in the same ways.
But this leads to some strange results. For a long time I would prepare a bowl of Corn Flakes every day, and every day my sleep-addled brain would say “Cork Flakes! Hee hee hee!”
Some mornings I make apple compote for the kids' breakfast. My brain never loses a chance to say “non compote mentis! Hee hee hee!” and it usually follows up with something about Truman Compote.
When I make grits, the brain usually ponders the kinship between “grits” and “groats”, and lately it has been considering the triphthong in an exaggerated Southern U.S. pronunciation of “grits”, which I discussed recently. The oatmeal is more fun. My brain always says something about goatmeal, and usually something else about stoatmeal.
I used to carry transit tokens and the first thing I would do after putting on my trousers would be to put two tokens into my pocket. My brain would mutter “tokens” and then “what if they were oaken tokens?”. At one point it started following this with “What if they were oaken tokens from Hoboken?”. I stopped using tokens a while ago, as they are being eliminated, and I am glad, because I don't think I want to know where the progression would go next.
When I see Rice Krispies in the cabinet, I always think of Bryce Crispus. I'm not sure who Bryce Crispus is and my brain never offers any additional information about him.
Toph sometimes has toast with Nutella and my brain always reminds me to think about the Nutelephone. (I work with someone named Michelle and it's always a little struggle not to mention the Michellephone, and then I started working with Liz Cortell, and the temptation grew almost too much to bear. But I will remain strong.)
When I cut up cucumbers to put into Katara's lunch, my brain usually makes a remark about how cucumbers should be followed with r-cumbers and s-cumbers. I tried typing that on my phone, and it took “qcumbers” in stride, but then it tried to autocorrect the next two to “qcumbers” also. I don't know, it's a mystery.
I have to put up with this nonsense every weekday morning.
Today I spent like ten minutes trying to think whether it was possible to find a subset of the real line that could be partitioned into an uncountable family of (nontrivial) intervals.
The answer is no, but it should have taken me way less than ten minutes to think of why. Each interval contains at least one rational number. Since the intervals are disjoint, there are not enough rational numbers to go around.
- singer
- finger
- ginger
THE ROAD TO WISDOM
The road to wisdom? — Well, it's plain
and simple to express:
Err
and err
and err again
but less
and less
and less.
(Piet Hein, Grooks 7. Hein was also the inventor of the Soma cube, the game of Hex, and the superellipsoid, among many other things.)
Emacs left behind an auto-save file, c/#computer-wizardry.blog#, and
every time I did git status -s I saw it mentioned. So I wanted to
tell Git to ignore this sort of file. (Sure, I could just remove the
file, but that's not the point.)
Git has a mechanism for telling it that certain files are
uninterresting and should never be tracked. You put patterns into
.git/info/exclude, and files whose names match the patterns are
ignored. I wanted to exclude all files whose names begin and and with
a # sign, so I put in:
#.*#
but this didn't work. I did cat .git/info/exclude and the line
wasn't there. “Wat” I said, and went to edit the file, and there it
was. I then realized that the default .git/info/exclude starts with
a big comment explaining how it works, that the comment lines all
start with #, that my new line also starts with #, so it is a
comment, so Git was ignoring it, and also I was ignoring it when I
did cat to view the file, and that's why I thought it wasn't there
at all. Sheesh.
So I escaped the # signs:
\#.*\#
and that also didn't work. Then I got out the manual and found that
you only need to escape a # sign at the start of a line, so I
changed it to:
\#.*#
and it still didn't work. At that point I gave up and moved on to doing something else.
Today I came back to it. I thought that a straight-up filename was matched by any file with that name in any subdirectory, but maybe I had that wrong, so I tried
*/#.*#
which ought to work at least for files one level down, but it didn't.
Then I consulted the manual again and found that ** will match any
sequence of directories, so I tried
**/#.*#
and that didn't work either. Then I tinkered with backslashing the #
signs various ways but nothing fixed the problem.
The problem was that I was using regex syntax .* instead of glob
syntax *. The right answer is:
\#*#
Just to be clear, this was not a problem with Git. It was a problem with me. Some days it pays to just stay in bed.
Sheesh.